Mediación y calculo de áreas y perímetros. (Serg)

La medición de las distancias, es decir, la determinación de las longitudes, el cálculo de áreas, o sea la obtención de superficies, y el manejo de espacios, es decir, las operaciones con volúmenes, requieren de la utilización de unidades adecuadas. Las que se comentan a continuación de unidades adecuadas. Las que se comentan a continuación corresponden al sistema métrico decimal, el más extendido en la actualidad.

Unidades para medir longitudes, áreas y volúmenes.

-La medida de una línea: longitud

Una cuerda puede ayudar a pensar en una línea: si la cuerda está tirante, dibujará muy aproximadamente una línea recta que se puede imaginar ilimitada, sin principio ni fin. Si se marca un punto en una recta, ésta queda dividida en dos semirrectas, una a cada lado del punto. Si se marcaron dos puntos, el fragmento de receta que queda limitado por ellos es u segmento.

Para saber cuál es el tamaño de un objeto, se procede a medirlo, operación que consiste en compararlo con otro objeto patrón, que sirve de unidad de medida: el número de veces que el objeto medido contiene la unidad tomada es la medida de dicho objeto.

Considérese un segmento de una línea cualquiera, no hace falta que sea una recta. Cuando se trata de medirlo, se parte de la suposición, de que es limitado, ya que de lo contrario no se podría medir. Para empezar, se toma como unidad otro segmento muy determinado, por ejemplo, un segmento llamado "centímetro". Se supone que el centímetro es flexible y que puede adaptarse al contorno de cualquier línea. Se procede a colocar el centímetro con un extremo sobre el del segmento que se quiere medir y se marca el punto al que llega el otro; se toma este último como como origen de una nueva superposición, y se repite el procedimiento dos, tres, cuatro veces, etc., hasta que se llega al final. Si se cuenta las veces que se ha superpuesto el centímetro sobre el segmento que se quiere medir, éste es el número que designa la longitud del segmento medido respecto de la unidad escogida.

-La medida de una superficie: su área:

Para tener una imagen del concepto de área, se puede utilizar la cara superior de un papel, cuya superficie es plana. Si se imagina una superficie plana sin límites y sin bordes, se estará pensando en un plano infinito. Si en un plano se dibujan un conjunto de líneas unidas formando una figura cerrada, el plano queda dividido en dos partes: la superficie comprendida dentro de la figura, y la que queda fuera de ésta. El fragmento de plano que queda dentro de la figura está limitado y es posible medir su superficie, es decir, saber como es de grande. Una vez se sabe cómo medir superficies comprendidas entre líneas, de forma general, se podrá medie la superficie, o lo que es lo mismo, el área, de un gran número de figuras geométricas distintas.

Como en el caso de la longitud, en la medida de superficies debe considerarse una unidad de medida. Para medir áreas, se toma como unidad de medida una superficie acotada bien definida: una unidad adecuada para para el dibujo ea un centímetro cuadrado, es decir, un cuadrado cuyos lados midan 1 cm de longitud. Para medir superficies, resulta útil disponer de una cuadrícula formada por una retícula de centímetros cuadrados. La medida de una superficie dibujada en la cuadrícula será el número de cuadraditos que obtenga.

-El sistema métrico decimal:

Para medir longitudes y superficies, conviene emplear un sistema de unidades homogéneas. Lo más es utilizar el sistema métrico decimal, en que, para medir longitudes, la unidad principal es el metro. Un metro (1 m) es una unidad de longitud cuyo tamaño está definido con gran precisión por la Oficina Internacional de Pesas y Medidas, con sede en Sèvres (Francia), organismo internacional ocupado de establecer distintas medidas.

Para medir longitudes reducidas, es útil emplear submúltiplos del metro: el decímetro (dm), que es la décima parte del metro; el centímetro (cm) y el milímetro (mm). Cada una de ellas el la décima parte de lo anterior. Para medir longitudes mayores, se usan múltiplos del metro: el decímetro (dam), que equivale a 10 metro; el hectómetro (hm) y el kilómetro (km). En el orden citado, cada una es 10 veces mayor que la anterior. Por orden de mayor a menor, se distribuye de la siguiente manera:

km    hm    dam    m    dm    cm    dm

Para medir superficies, por ejemplo la extensión de un campo o las paredes de una habitación, en el sistema métrico decimal se toma como medida básica el metro cuadrado (m²), definido como el área de un cuadrado cuyos lados miden 1 m. Por orden de mayor a menor, la serie de unidades de medida de áreas es:

km²    hm²    dam²    m²    dm²    cm²    mm²

Para medir el volumen de un cuerpo, es decir, la porción del espacio tridimensional que ocupa, se toma como medida básica el metro cúbico (m³). Un metro cúbico es es el volumen de un cubo cuyas caras son cuadrados de 1 m de lado. Como en los casos de las unidades de longitud y de superficie, existen múltiplos y submúltiplos del metro cúbico. La serie ordenada de mayor a menor, es como sigue:

km³    hm³    dam³    m³    dm³    cm³    mm³

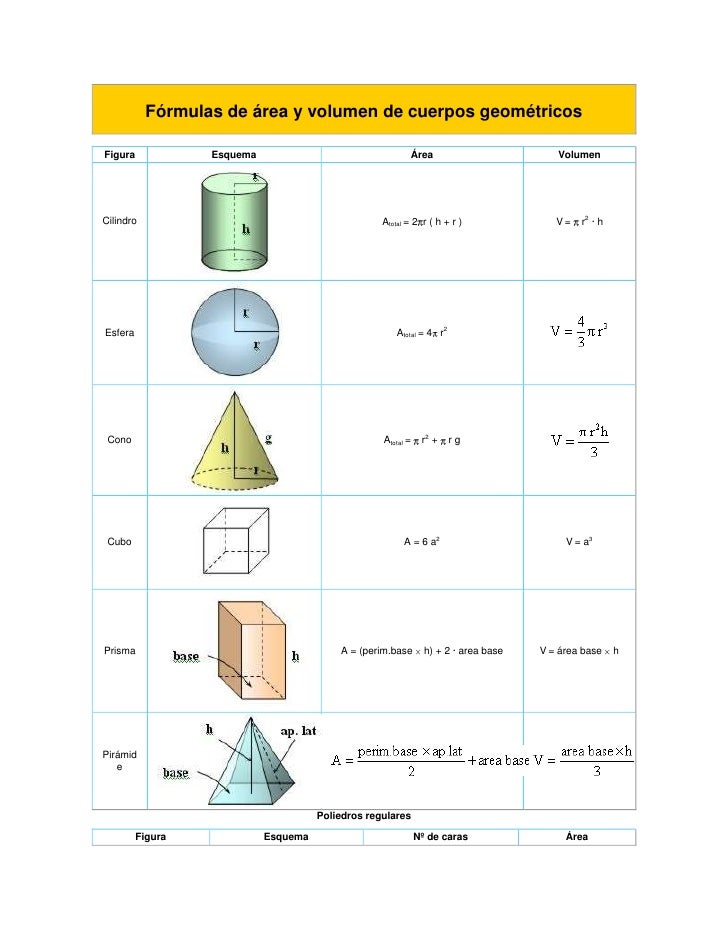
Formula de cuerpos geometricos

-Perímetro, área, y volumen:

1. El perímetro de un polígono (o cualquier otra curva cerrada, tal como un círculo) es la distancia alrededor del exterior.

2. El área de una curva simple, cerrada, plana es la cantidad del espacio interior.

3. El volumen de un solido de forma 3D es la cantidad del espacio desplazado por el.

Algunas fórmulas para figuras planas comunes de 2 dimensiones y solidos de 3 dimensiones se dan a continuación. Las respuestas tienen una, dos, o tres dimensiones; el perímetro es medido en unidades lineales, el área es medido en unidades cuadradas , y el volumen es medido en unidades cúbicas.